Démonstration : Organisation en rhombes
Pour mener à bien cette étude, nous ne considèrerons qu'un alvéole.
On ne s’interesse dans cette démonstration qu'uniquement à un tier du prisme originel
composant l'alvéole d'abeille..
Nous tenterons de montrer les différences entre l'organisation spécifique des abeilles (en
rhombes) et l'utilisation de prisme complet classique.
Hypothèse
Soit un prisme dont les couvercles sont deux hexagones H et H'.
K est le tier de prisme naturel de couvercle le losange OABC.
L est le tier de prisme tronqué de couvercle le losange SAB’C.
A, B et C sont trois sommets consécutifs de H.
O est le centre de H.
D, E et F sont les points de H' opposés respectivement à A,B et C.
Soit S tel que SAB'C soit un losange.
On pose 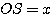 et
et


I-Comparaison des volumes
Dans un premier temps, nous tenterons de comparer les volumes des deux polyèdres.
Par hypothèses, 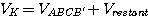
Et


Le polyèdre étudié est un prisme dont les couvercles sont des hexagones réguliers.
Donc par définition, on a
 <.>
<.>
Donc  est un losange.
est un losange.
Donc ses diagonales se coupent en leur milieu et sont perpendiculaires.
Soit  ;leur point
d'intersection,
;leur point
d'intersection,
Donc  est le milieu
de
est le milieu
de  et
et
 .
.
Soit  la rotation de centre
la rotation de centre
 et d'angle
et d'angle
 ,
,
Donc  et
et
 et
et
 .
.
 est un losange,
est un losange,
Donc ses diagonales se coupent en leur milieu et sont parallèles.
Or  milieu de
milieu de
 ,
,
Donc  milieu de
milieu de
 .
.
Donc  .
.
 ,
,
 ,
,
 et
et
 ,
,
Donc l'image du tétraèdre  est
le tétraèdre
est
le tétraèdre  .
.
 est une rotation donc
est une rotation donc
 est une isométrie,
est une isométrie,
Donc  est une similitude de
rapport
est une similitude de
rapport  .
.
Donc par propriété,  .
.
Ainsi, 
De ce fait, le choix d'une des deux structures n'influe pas sur le volume total de
l'alvéole.
Nous chercherons alors à trouver une différenciation au niveau des aires exterieures de pour
chacune des possibilités de construction.
II-Comparaison des aires

Ainsi, nous essayerons désormais de comparer les aires exterieures des deux structures.
Pour cela, il nous est tout d'abord nécessaire de réaliser quelques calculs de distances.
On pose 
Donc 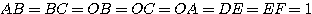
Nous avons pu voir que G était le milieu de
 et
et

Donc 
Et 
Donc 

Or  et
et

donc 
Donc GAB est un triangle rectangle en G
Donc d’après le théorème de Pythagore,

Donc 
Donc 
Donc 
Or 
Donc 
 est un losange
est un losange
Donc ses cotés sont egaux donc

 est un face du prisme donc
c'est un rectangle
est un face du prisme donc
c'est un rectangle
Donc le triangle  est rectangle en
B.
est rectangle en
B.
Donc d'après le théorème de Pythagore, on a
 .
.
Nous avons pu voir dans la partie précedente que
 et
et

Or  est une isométrie donc
est une isométrie donc

Donc 
Donc 
Et 

Donc 
Donc 
Or  et
et
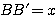
Donc 
SAB’C est un losange
Donc ses diagonales se coupent en leur millieux et sont orthogonales
Donc 
Or  est le milieu de
est le milieu de
 et de
et de

donc 
donc le triangle  est rectangle
en
est rectangle
en 
donc d’après le théoreme de Pythagore

Donc 
Donc 
Donc 
Donc 
Donc 
Or 
Donc 
Déterminons l’Aire de K
Nous allons donc maintenant calculer l'aire du tier de prisme non coupé.
Par hypothèse, 
 est un face latérale du
prisme donc c'est un rectangle
est un face latérale du
prisme donc c'est un rectangle
Donc 
Or 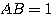 et BE est une arète latéral du
prisme
et BE est une arète latéral du
prisme
Donc 
Donc 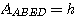 (1)
(1)
 est aussi une face latérale du
prisme
est aussi une face latérale du
prisme
Donc par un raisonement analogue, on trouve
 (2)
(2)
 est losange
est losange
Donc 
Or  et
et

Donc  (3)
(3)
Ainsi, d'après (1), (2) et (3), on trouve

Déterminons l'aire de L
Nous allons désormais calculer l'aire exterieure du prisme modifié.
Par hypothèse, 
SAB’C est un losange
Donc 
Or  et
et

Donc 
Donc  (1)
(1)
ADEB' est un trapèze
Donc 
Or  et
et

Donc 
Donc  (2)
(2)
B'DFC est un trapèze.
Donc 
Par un raisonement analogue, on trouve
 (3)
(3)
Avec  et (3) on trouve
et (3) on trouve

Ainsi, l'aire de  dépend de la
variable
dépend de la
variable  .
.
Pour l'étudier, nous devons donc associer une fonction à cette aire.
On pose 
Donc 
 est une distance donc
est une distance donc
 definie sur
definie sur

Dérivons 
 est dérivable sur
est dérivable sur


Donc 
Donc 
Cherchons le signe de cette dérivée

Donc  est du signe de
est du signe de



 donc
donc

et 
La fonction carré est croissante sur 
Donc 
Donc 
Donc 
Donc 
Donc 
Donc 
Donc  pour
pour

Et  pour
pour

Donc  est décroissante pour
est décroissante pour
 et
et
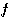 est croissante pour
est croissante pour

Ces résultats peuvent être résumés dans un tableau de variation de la fonction
 .
.

Ainsi la fonction  admet un minimum en
admet un minimum en


Donc 
Donc 
Donc 
Donc 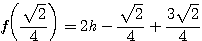
Donc 
Or 
Donc 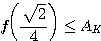
Ainsi pour une grandeur donnée, l'aire de L est inferieure à l'aire de K.
Pour cette valeur, la structure employé par les abeilles apparait alors comme la plus
économique.
Nous pourrions alors nous demander pour quelles valeurs de
 l'aire de L est infèrieure a l'aire
de K
l'aire de L est infèrieure a l'aire
de K
Cela se traduit par l'inéquation 
 :
:



Or  donc
donc

Et 
La fonction carré est croissante sur

Donc 
Donc 
Donc 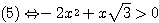
On pose 
 est une fonction polynome de
discriminant
est une fonction polynome de
discriminant 

Donc 
 donc les racines de
donc les racines de
 sont
sont
 et
et
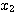
 et
et

Donc  et
et

Donc  et
et

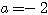 donc
donc

 est du signe de
est du signe de
 à l'éxterieur des racines et du
signe opposé à l'interieur
à l'éxterieur des racines et du
signe opposé à l'interieur
Donc  pour
pour

Donc 
Ainsi, l'aire de K est infèrieure a l'aire de L si et seulement si
 est compris
entre
est compris
entre et
et


(Cette étude a été menée en prenant pour hypothèse de base AB=1
La valeur limite est donc de 0.471404*AB pour la longueur de OS.
Pour une valeur de OS comprise entre 0 et 0.471404AB , les abeilles ont intérêts a
utiliser cette forme d'alvéole en raison de l'aire extèrieure qui est infèrieure à celle d'une
structure classique en hexagone.)
Valeurs des angles
Par un calcul d'angle, nous pouvons parvenir à trouver la valeur approchée de


On se propose alors de calculer la valeur de l'angle
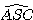 pour
pour

Dans le triangle  , on utilise
la formule d'Al-Kashi,
, on utilise
la formule d'Al-Kashi,
Ainsi, 
Or 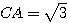 et
et

Avec  , on trouve
, on trouve

Donc 
Donc 
Donc 
Donc 
Ainsi, on trouve 
Cette valeur des angles est proche de celle que de fameux mathématiciens avait trouvé par des
méthodes différentes de celle-ci.
En cela, nous trouvons une valeur de
 de
de
 .
.
Or  est le minimum de la
fonction
est le minimum de la
fonction 
Donc cela confirme le fait que les abeilles utilisent le rapport de distance qui permet d'avoir
la plus petite aire.
Par cela, elles font la plus grande économie de cire possible.
Finalement, nous avons bien montré à l'aide de ces deux raisonnements, que les
alvéoles d'abeille présentent une forme particulière favorisant l'économie de cire, d'une part
par l'emploi de l'hexagone, pavant le plan sans perte avec un périmètre réduit, et d'autre part
avec l'emploi d'un fond en losanges, garant d'une surface externe minimum. Il s'agit donc d'une
struture des plus ingénieuses.